Category Basics

It seems inevitable that, after one learned Haskell, there’s a good possibility she will become a victim of category theory. This is a series(hopefully) of notes about category theory.

Category Theory is the theory using formal method to study the semantics of cats a language that is spoken by mathematicians, just like Design Pattern is a language spoken by senior software engineers. Of course, the latter one reads less exotic and sometimes harmful.

Definition of Category

A category \(C\) consists of:

• A collection of objects, \(\text{Ob}(C)\);

• A collection of morphisms(arrows), \(\text{Mor}(C)\);
  • For each morphism(arrow) \(f\), a domain object \(A\) and a codomain object \(B\). \(f:A\rightarrow B\) and \(dom(f)=A, cod(f)=B\).
  • The collection of morphisms(arrows) between two objects: domain \(A\) and codomain \(B\), is denoted as \(\text{Hom}(A, B)\).
• A binary operator $\circ$ called composition, satisfying:
  • For any pair of arrows \(f:A\rightarrow B\) and \(g:B\rightarrow C\), an arrow \(g\circ f:A\rightarrow C\).
  • (Associativity) For any \(f:A\rightarrow B, g: B\rightarrow C, h:C\rightarrow D\), we have \(h\circ(g\circ f)=(h\circ g)\circ f\).
  • (Identity) For each object \(A\), an identity arrow \(id_A\), such that for any arrow \(f\), \(id_{A}\circ f=f=f\circ id_{A}\).

Examples of Category

1. \[\textbf{Set}\]

   • Objects: sets, \(A\).

   • Arrows: total functions, \(f:A\rightarrow B\).
   • Composition: function composition.
2. \[\textbf{Poset}\]
   • Objects: partially-ordered sets, \((P,\leq)\).
     • \(P\) is a set.
     • \(\leq\) is a reflexive, transitive, antisymmetric relation on $P$.
   • Arrows: total order-preserving functions, \(f:P\rightarrow Q\), such that \(\forall p,p'\in P.p\leq_{P}p' \rightarrow f(p)\leq_{Q} f(p')\).
   • Composition: function composition.
3. \[\textbf{Mon}\]
   • Objects: monoids, \((M,\cdot)\).
     • \(M\) is a set.
     • \(\cdot\) is an associative binary operator on \(M\).
     • an identity element \(e\in M\) such that \(\forall m\in M.e\cdot m=m=m\cdot e\).
   • Arrows: monoid homomorphisms, \(f:M\rightarrow N\), such that \(\forall m,m'\in M.m\cdot_{M}m'=f(m)\cdot_{N}f(m')\) and \(f(e_{M})=e_{N}\).
   • Composition: homomorphism composition.
4. \[\textbf{Grp}\]
   • Objects: group, \((G,\cdot)\)
     • \(G\) is a set.
     • \(\cdot\) is an associative binary operator.
     • an identity element \(e\in G\) such that \(\forall g\in G.g\cdot e=g=e\cdot g\).
     • inverse: \(\forall g\in G.\exists g^{-1}\in G.g\cdot g^{-1}=e=g^{-1}\cdot g\).
   • Arrows: group homomorphisms, \(f:G\rightarrow H\), such that \(\forall g,g'\in G.g\cdot_G g'=f(g)\cdot_H f(g')\), \(f(e_M)=e_N\)
   • Composition: homomorphism composition.
5. \[\textbf{Ω-Alg}\]
   • Objects: Ω-Algebras, \((\vert A\vert, a)\).
     • \(\vert A\vert\) is a set called carrier.
     • \(a:\sum_{\omega\in\Omega}\vert A\vert^{ar(\omega)}\rightarrow\vert A\vert\) is an interpretation.
       • \(\Omega\) is a set of operator (signature).
       • \(ar(\omega)\) is the arity of \(\omega\).
   • Arrows: \(\Omega\)-homomorphisms, \(h:\vert A\vert\rightarrow\vert B\vert\), such that \(\forall\omega\in\Omega.h\left(a(x_1,...,x_{ar(\omega)})\right)=b\left(h(x_1),...,h(x_{ar(\omega)})\right)\).
   • Composition: homomorphism composition.

More examples:

• Categorical Logic

  • Objects: formulas, \(A\).

  • Arrows: proofs, \(f:A\rightarrow B\).

  • Composition: transitivity of implication. \(\begin{prooftree} \AxiomC{$f:A\rightarrow B$} \AxiomC{$g:B\rightarrow C$} \BinaryInfC{$g\circ f:A\rightarrow C$} \end{prooftree}\)

• Functional Programming Language
  • Objects: types, \(T\).
  • Arrows: functions, \(f: T\rightarrow U\)
  • Composition: function composition
• Dual Category \(\textbf{C}^{\textbf{op}}\) of \(\textbf{C}\)
  • Objects: \(\text{Ob}(\textbf{C})\)
  • Arrows: opposite of arrows in \(\textbf{C}\).
    • \(\forall f:A\rightarrow B\) from \(\textbf{C}\), we have \(f^{op}:B\rightarrow A\) in \(\textbf{C}^{\textbf{op}}\)
  • Composition: trivial.
• Product category \(\textbf{C}\times\textbf{D}\)
  • Objects: objects pairs \((A, B)\) where \(A\) is a \(\textbf{C}\)-object and \(B\) is a \(\textbf{D}\)-object.
  • Arrows: arrows pairs \((f,g)\) where \(f\) is a \(\textbf{C}\)-arrow and \(g\) is an \(\textbf{D}\)-arrow.
  • Composition: pairwise composition, \((f,g)\circ(h,i)=(f\circ h,g\circ i)\).
• Subcategory \(\textbf{B}\) of \(\textbf{C}\)
  • Objects: each \(\textbf{B}\)-object in is a \(\textbf{C}\)-object
  • Arrows: for all \(\textbf{B}\)-objects \(B\) and \(B'\), \(\text{Hom}_B(B,B')\subseteq \text{Hom}_C(B,B')\)
  • Composition: same as \(\textbf{C}\)

Commutative Diagrams

Definition

A diagram in a category \(\textbf{C}\) is a collection of vertices and directed edges, consistently labeled with objects and arrows of \(\textbf{C}\).

A diagram is said to commute if for every pair of objects \(X,Y\), all the paths from \(X\) to \(Y\) are equal.

Example

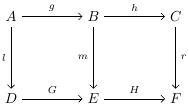
This diagram commutes:

• In the inner left squre: \(m\circ g=G\circ l\)
• In the inner right squre: \(r\circ h=H\circ m\)
• In the outer rectangle: \(r\circ h\circ g=H\circ G\circ l\)